When measuring and managing credit risk, It is important to have a clear understanding of common terms such as expected loss and unexpected loss. As stated in Credit Risk Assessment, credit risk is defined as “the potential that a bank borrower or counterparty will fail to meet its obligations in accordance with agreed terms.” This article will explain the calculations for expected loss (EL) and unexpected loss (UL), for both an individual asset and for a portfolio. Additionally, risk contribution (RC) will be defined.
To begin, let’s review the common terminology used in these calculations:
Terminology
- Probability of Default (PD) – is the likelihood that a loan will not be repaid and will fall into default. It must be calculated for each borrower. The credit history of the borrower and the nature of the investment must be taken into consideration when calculating PD. External ratings agencies such as Standard & Poors or Moody’s may be used to get a PD; however, banks can also use internal rating methods. PD can range from 0% to 100%. If a borrower has 15% PD it is considered a less risky company vs. a company with a 30% PD.
- Adjusted Exposure (AE) – is equal to outstanding loan amount (OS) plus the percentage of unused loan commitment (COM) drawn-down by the borrower; known as the usage given default (UGD). AE is calculated as follows:
AE = OS + (COM – OS) * (UGD)
- Recovery Rate (RR) – the proportion of a bad debt that can be recovered.
- Loss Given Default (LGD) – the credit loss incurred if an obligor of the bank defaults. LGD = 1- RR
- Expected Default Frequency (EDF) – refer to Probability of Default
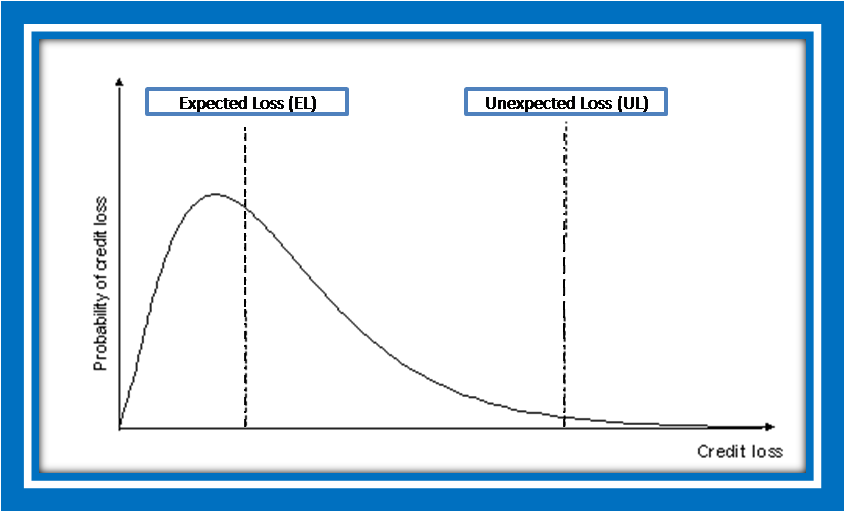
- Expected Loss (EL) – referring back to Expected Loss Calculation, EL is the loss that can be incurred as a result of lending to a company that may default. It is the average loss in value over a specified period.
- Unexpected Loss (UL) – it is known as the variation in expected loss. UL is typically larger than EL but they are both equal to zero when PD is zero.
Expected Loss (EL)
EL for a single asset is calculated by using the following formula:
EL = AE * LGD * EDF
To calculate EL for a portfolio we must add the expected losses of the individual assets; formula below:
ELP = ∑ELi
Unexpected Loss (UL)
UL for a single asset is calculated by using the following formula:
UL = AE * SQRT [(EDF * σ²LGD) + (LGD² * σ²EDF)]
To calculate the UL for a portfolio, we need to use a more complex formula. Below is the formula for a 2 asset portfolio:
ULP = SQRT [ULi² + ULj² + 2 (ρi,j) (ULi) (ULj)]
Note: The UL of the portfolio will be less than the sum of the ULs for the individual assets due to diversification benefits.
Risk Contribution
Each asset in a portfolio contributes a portion of its UL to the portfolio UL; known as risk contribution (RC). In other words, it is the incremental risk that the exposure of a single asset contributes to the total risk of the portfolio. The formula for calculating the RC of asset i and j for a two asset portfolio is illustrated below:
RCi = ULi * [ULi + (ρi,j) * (ULj) / ULp]
RCj = ULj * [ULj + (ρi,j) * (ULi) / ULp]
If we take the sum of RCi + RCj we will get the same value as the unexpected loss on the portfolio.
Correlation (ρ) plays an important role in measuring the potential UL in the portfolio. If correlation between the assets increases, the potential UL will increase.
Sources:
Financial Risk Manager Handbook: (Fifth Edition) Philippe Jorion Introduction to Credit Risk (pg 434)
Wharton: What Do We Know About Loss Given Default? Til Schuermann